Normed Vector Spaces

Definition 2

A normed vector space is a vector space \(\mathcal{V}\) with a function \(\lVert\cdot\rVert:\mathcal{V}\rightarrow \mathbb{R}_+\), called norm, satisfying the following properties for all \(\vvec{v},\vvec{w}\in\mathcal{V}\) and \(\alpha\in\mathbb{R}\):

\[\begin{align*} \lVert \vvec{v}+\vvec{w}\rVert &\leq\lVert\vvec{v}\rVert +\lVert\vvec{w}\rVert &\text{(triangle inequality)}\\ \lVert \alpha\vvec{v}\rVert &=\lvert\alpha\rvert\lVert\vvec{v}\rVert &\text{(homogeneity)}\\ \lVert\vvec{v}\rVert =0&\Leftrightarrow \vvec{v}=\vvec{0} \end{align*}\]

The norm measures the length of vectors.

Example 3

The \(d\)-dimensional Euclidean space is the space of \(\mathbb{R}^d\) with the Euclidean norm:

\[\lVert \vvec{v}\lVert_2 = \lVert \vvec{v}\rVert =\sqrt{\sum_{i=1}^d v_i^2}\]

The Euclidean norm computes the length of a vector by means of the Pythagorean theorem:

\[\lVert \vvec{v}\rVert^2 = v_1^2 + v_2^2\]

The Euclidean norm introduces a geometric interpretation of the inner product of two vectors. The inner product is defined by the lengths of the vectors and the cosine of the angle between them.

\[\begin{align*} \vvec{v}^\top\vvec{w} = \sum_{i=1}^dv_iw_i = \cos\sphericalangle(\vvec{v},\vvec{w})\lVert\vvec{v}\rVert\lVert\vvec{w}\rVert \end{align*}\]

In Machine Learning, the inner product is often used as a similarity measure between two points. The idea is that two points facing in the same direction have a cosine close to one, and hence a larger inner product than two points looking into distint directions. If two vectors are orthogonal, then \(\cos\sphericalangle(\vvec{v},\vvec{w})=0\) and the inner product is zero

\[\begin{align*} \vvec{v}^\top\vvec{w} &= \cos\sphericalangle(\vvec{v},\vvec{w})\lVert\vvec{v}\rVert\lVert\vvec{w}\rVert =0 \end{align*}\]

Two vectors are called orthonormal if they are orthogonal and have unit norm \(\lVert \vvec{v}\rVert = \lVert\vvec{w}\rVert =1\).

Theorem 2

The inner product of a vector \(\vvec{v}\) and a normalized vector \(\frac{\vvec{w}}{\lVert\vvec{w}\rVert}\) computes the length of the projection \(\vvec{p_v}\) of \(\vvec{v}\) onto \(\vvec{w}\). Using the notation of vectors from the image below, we have

\[\begin{align*} \lVert\vvec{p}_v\rVert = \vvec{v}^\top \frac{\vvec{w}}{\lVert\vvec{w}\rVert} \end{align*}\]

Proof. From the definition of the cosine in a triangle follows that

\[\begin{align*} \cos(\phi)= \frac{\lVert\vvec{p}_v\rVert}{\lVert \vvec{v}\rVert} &\Leftrightarrow \lVert \vvec{p}_v\rVert =\cos(\phi)\lVert \vvec{v}\rVert =\vvec{v}^\top \frac{\vvec{w}}{\lVert \vvec{w}\rVert} \end{align*}\]

Example 4 (Manhattan norm)

The Manhattan norm is defined as:

\[\lVert \vvec{v}\lVert_1 = \lvert \vvec{v}\rvert =\sum_{i=1}^d \lvert v_i\rvert\]

The Manhattan norm computes the length of a vector coordinate-wise:

\[\lvert \vvec{v}\rvert = \lvert v_1\rvert + \lvert v_2\rvert\]

Example 5 (\(L_p\)-norms)

For \(p\in[1,\infty]\), the function \(\lVert\cdot\rVert_p\) is a norm, where

\[\begin{align*} \lVert \vvec{v}\lVert_p & =\left(\sum_{i=1}^d \lvert v_i\rvert^p\right)^{1/p} \end{align*}\]

The two-dimensional circles \(\{\vvec{v}\in\mathbb{R}^2\vert \lVert\vvec{v}\rVert_p =1\}\) look as follows:

So, the norm measures the length of a vector. Can we also measure the length of a matrix?

Yes, matrix norms are the same but different.

Definition 3 (Matrix norms)

We can extend the \(L_p\) vector normes to the element-wise \(L_p\) matrix norms:

\[\begin{align*} \lVert A\lVert_p & =\left(\sum_{i=1}^n\sum_{j=1}^m \lvert A_{ji}\rvert^p\right)^{1/p} \end{align*}\]

Furthermore, we introduce the operator norm

\[\begin{align*} \lVert A\rVert_{op} &=\max_{\lVert \vvec{v}\rVert=1} \lVert Av\rVert \end{align*}\]

Definition 4 (Trace)

The trace sums the elements on the diagonal of a matrix. Let \(A\in\mathbb{R}^{n\times n}\), then

\[\tr(A) = \sum_{i=1}^n A_{ii}\]

1. \(\tr(cA+B)=c\tr(A)+\tr(B)\) (linearity)

2. \(\tr(A^\top)=\tr(A)\)

3. \(\tr(ABCD)=\tr(BCDA)=\tr(CDAB)=tr(DABC)\) (cycling property)

For any vector \(\vvec{v}\in\mathbb{R}^d\) and matrix \(A\in\mathbb{R}^{n\times d}\), we have

\[\begin{align*} \lVert\mathbf{v}\rVert^2 &= \mathbf{v}^\top \mathbf{v} = \tr(\mathbf{v}^\top \mathbf{v}) &\lVert A\rVert^2 &= \tr(A^\top A) \end{align*}\]

From this property derive the binomial formulas of vectors and matrices:

\[\begin{align*} \lVert \vvec{x}-\vvec{y}\rVert^2 &= ( \vvec{x}-\vvec{y})^\top(\vvec{x}-\vvec{y}) = \lVert\vvec{x}\rVert^2 -2\langle\vvec{x},\vvec{y}\rangle +\lVert\vvec{y}\rVert^2\\ \lVert X-Y\rVert^2 &= \tr( (X-Y)^\top(X-Y)) = \lVert X\rVert^2 -2\langle X, Y\rangle +\lVert Y\rVert^2 \end{align*}\]

Orthogonal Matrices

A matrix \(A\) with orthogonal columns satisfies

\[\begin{align*} A^\top A = \diag(\lVert A_{\cdot 1}\rVert^2, \ldots, \lVert A_{\cdot d}\rVert^2) \end{align*}\]

A matrix \(A\) with orthonormal columns satisfies

\[\begin{align*} A^\top A = \diag(1, \ldots, 1) \end{align*}\]

A square matrix \(A\in \mathbb{R}^{n\times n}\) is called orthogonal if

\[A^\top A = AA^\top=I\]

A vector norm \(\lVert\cdot \rVert\) is called orthogonal invariant if for all \(\vvec{v}\in\mathbb{R}^n\) and orthogonal matrices \(X\in\mathbb{R}^{n\times n}\) we have

\[\lVert X\vvec{v}\rVert = \lVert \vvec{v}\rVert\]

A matrix norm \(\lVert\cdot \rVert\) is called orthogonal invariant if for all \(V\in\mathbb{R}^{n\times d}\) and orthogonal matrices \(X\in\mathbb{R}^{n\times n}\) we have

\[\lVert XV\rVert = \lVert V\rVert\]

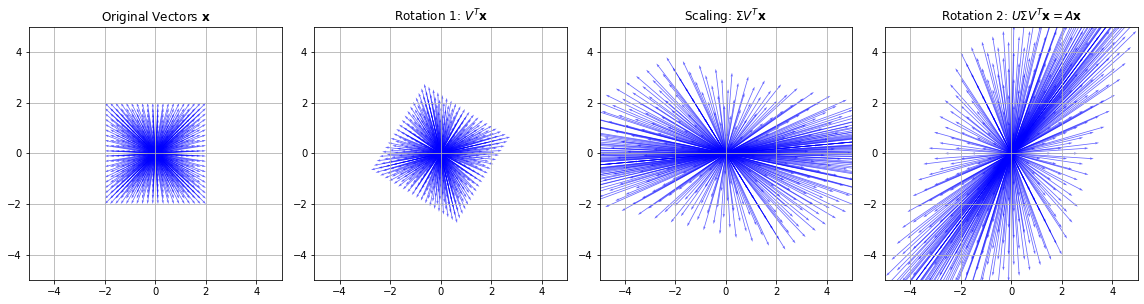
Theorem 3 (SVD)

For every matrix \(X\in\mathbb{R}^{n\times p}\) there exist orthogonal matrices \(U\in\mathbb{R}^{n\times n}, V\in\mathbb{R}^{p\times p}\) and \(\Sigma \in\mathbb{R}^{n\times p}\) such that

\[X= U\Sigma V^\top, \text{ where}\]

• \(U^\top U= UU^\top=I_n, V^\top V=VV^\top= I_p\)

• \(\Sigma\) is a rectangular diagonal matrix, \(\Sigma_{11}\geq\ldots\geq \Sigma_{kk}\) where \(k=\min\{n,p\}\)

The column vectors \(U_{\cdot s}\) and \(V_{\cdot s}\) are called left and right singular vectors and the values \(\sigma_i=\Sigma_{ii}\) are called singular values \((1\leq i\leq l)\).

A = np.random.rand(4,2)
U, σs,Vt = linalg.svd(A)
print(U.shape, σs.shape, Vt.shape)

(4, 4) (2,) (2, 2)

U

array([[-0.6, -0.1, -0.5, -0.6],
       [-0.4, -0.8,  0.4,  0.1],
       [-0.5,  0.5,  0.7, -0.3],
       [-0.5,  0.2, -0.2,  0.8]])

U@U.T

array([[ 1.0e+00, -1.6e-16, -4.3e-16, -2.6e-16],
       [-1.6e-16,  1.0e+00,  3.1e-17, -5.4e-17],
       [-4.3e-16,  3.1e-17,  1.0e+00, -1.7e-16],
       [-2.6e-16, -5.4e-17, -1.7e-16,  1.0e+00]])

np.diag(σs)

array([[2.1, 0. ],
       [0. , 0.6]])

Σ = np.row_stack( (np.diag(σs),np.zeros((2,2))) )
Σ

array([[2.1, 0. ],
       [0. , 0.6],
       [0. , 0. ],
       [0. , 0. ]])

A \((n\times n)\) matrix \(A=U\Sigma V^\top\) is invertible if all singular values are larger than zero. The inverse is given by

\[A^{-1} = V \Sigma^{-1} U^\top,\ \text{ where }\]

\[\begin{align*} \Sigma=\begin{pmatrix}\sigma_1 & 0 & \ldots & 0 \\ 0 & \sigma_2 &\ldots & 0\\ & & \ddots &\\ 0 & 0 & \ldots & \sigma_n\end{pmatrix},\qquad \Sigma^{-1}= \begin{pmatrix}\frac{1}{\sigma_1} & 0 & \ldots & 0 \\ 0 & \frac{1}{\sigma_2} &\ldots & 0\\ & & \ddots &\\ 0 & 0 & \ldots & \frac{1}{\sigma_n}\end{pmatrix} \end{align*}\]

Since the matrices \(U\) and \(V\) of the SVD are orthogonal, we have:

\[\begin{align*} AA^{-1} &= U\Sigma V^\top V\Sigma^{-1} U^\top = U\Sigma \Sigma^{-1} U^\top = UU^\top = I\\ A^{-1}A &= V \Sigma^{-1} U^\top U\Sigma V^\top = V \Sigma^{-1} \Sigma V^\top = V V^\top = I \end{align*}\]

import numpy as np
import matplotlib.pyplot as plt

# Create a grid of vectors (2D plane)
x = np.linspace(-2, 2, 20)
y = np.linspace(-2, 2, 20)
X, Y = np.meshgrid(x, y)
vectors = np.stack([X.ravel(), Y.ravel()], axis=0)

# Define a matrix A (non-symmetric, non-orthogonal)
A = np.array([[2, 1],
              [1, 3]])

# Compute SVD: A = U Σ V^T
U, S, VT = np.linalg.svd(A)
Sigma = np.diag(S)

# Decompose transformations
V = VT.T
rotation1 = V
scaling = Sigma
rotation2 = U

# Apply transformations step-by-step
V_vectors = rotation1 @ vectors
S_vectors = scaling @ V_vectors
U_vectors = rotation2 @ S_vectors  # Final result: A @ vectors

# Plotting setup
fig, axs = plt.subplots(1, 4, figsize=(16, 4))

def plot_vectors(ax, vecs, title):
    ax.quiver(np.zeros_like(vecs[0]), np.zeros_like(vecs[1]),
              vecs[0], vecs[1], angles='xy', scale_units='xy', scale=1,
              color='blue', alpha=0.6)
    ax.set_xlim(-5, 5)
    ax.set_ylim(-5, 5)
    ax.set_aspect('equal')
    ax.set_title(title)
    ax.grid(True)

# Plot each step
plot_vectors(axs[0], vectors, "Original Vectors $\mathbf{x}$")
plot_vectors(axs[1], V_vectors, "Rotation 1: $V^T\mathbf{x}$")
plot_vectors(axs[2], S_vectors, "Scaling: $\Sigma V^T\mathbf{x}$")
plot_vectors(axs[3], U_vectors, "Rotation 2: $U\Sigma V^T\mathbf{x}=A \mathbf{x}$")

plt.tight_layout()
plt.show()