Teaching
I created the following lectures for a Bachelor level course about data mining and machine learning at TU/e. For every lecture, there are videos (to see them expand the corresponding lecture item), slides and a Proofs, Exercises and Literature (PELi) document. Some lectures have additionally a Python notebook.
Linear Algebra - Recap
vectors - matrices - matrix multiplication - vector and matrix norms - SVD
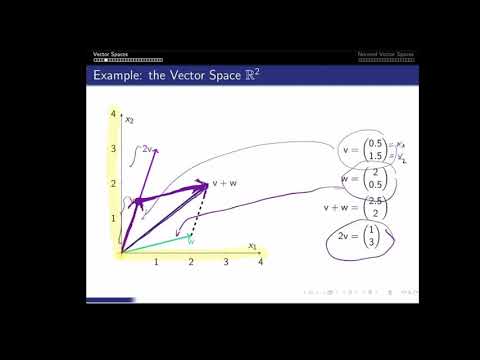
Part 1: Vectors and Matrices
- Vector spaces
- The transposed of a matrix
- Symmetric and diagonal matrices
Part 2: Matrix Multiplication
- The inner and outer product of vectors
- Matrix multiplication: inner and outer product-wise
- Identity matrix and inverse matrices
- Transposed of a matrix product

Part 3: Vector Norms
- The Euclidean norm and the inner product
- Orthogonal vectors
- Vector Lp-norms

Part 4: Matrix Norms
- Matrix Lp-norms and the operator norm
- Orthogonal matrices
- Orthogonal invariance of matrix norms
- The trace
- Binomial formulas for norms
- Singular Value Decomposition and invertibility of a matrix

Optimization
FONC & SONC - numerical optimization - convexity - gradients
Part 1: FONC & SONC
- Unconstrained optimization objectives
- First Order Necessary Condition (FONC) for minimizers
- Second Order Necessary Condition (SONC) for minimizers
- Finding stationary points of smooth functions

Part 2: Numerical Optimization
- Constrained optimization objectives
- Gradient Descent
- Coordinate Descent

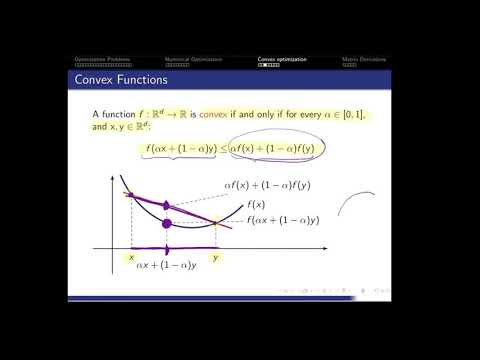
Part 3: Convexity
- Convex sets
- Convex functions
- Convex optimization problems
Part 4: Computing Gradients
- Partial derivatives, the gradient and the Jacobian
- Linearity of gradients
- Chain rule

Regression
regression with basis functions - bias-variance tradeoff - cross validation
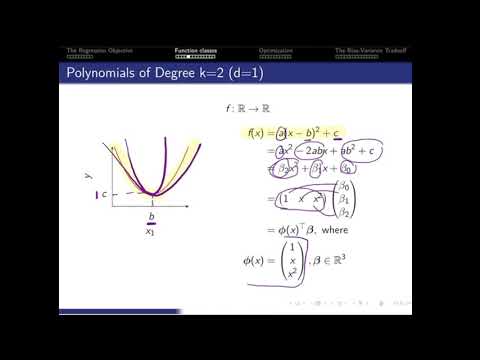
Part 1: The Regression Objective
- Formal regression task definition
- Affine regression functions
- Polynomial regression functions
- Radial Basis regression functions
Part 2: Regression Optimization
- Residual Sum of Squares (RSS)
- Design matrix
- Solving the regression problem
- The set of global regression minimizers

Part 3: The Bias-Variance Tradeoff in Regression
- Evaluating the regression model
- The Mean Squared Error (MSE)
- Splitting in test- and training dataset
- The Expected Prediction Error (EPE)
- Bias, variance and noise of a regression model and the bias-variance tradeoff
- Cross-validation

Regularization in Regression
regression in high dimensional feature spaces - ridge regression - Lasso
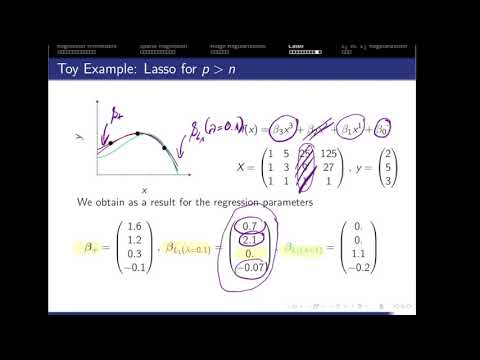
Part 1: p larger n
- Determining the set of global minimizers by SVD
- Python implementation

Part 2: Sparse Regression
- The sparse regression objective
- Relaxing the sparse regression objective
- Lp-norm regularization

Part 3: Ridge Regression
- The ridge regression objective
- The minimizer of ridge regression

Part 4: Lasso
- The Lasso objective
- The coordinate descent optimization of Lasso
- Comparison of L1 and L2 regularization
slides PELi PELi Solutions Notebook
Recommender Systems and Dimensionality Reduction
matrix factorization - matrix completion - PCA
Part 1: The Rank-r Matrix Factorization Problem
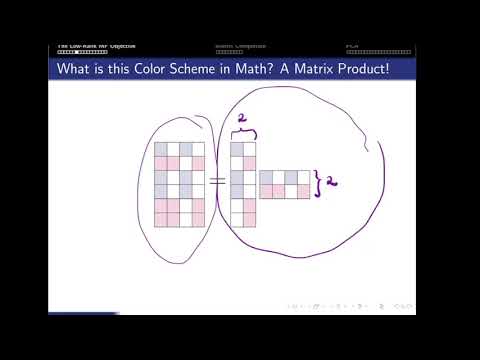
- Summarizing user behavior via a matrix product
- The matrix factorization objective
- Truncated SVD as the solver for the rank-r MF problem
- Nonconvexity of the objective
Part 2: Matrix Completion
- Handling missing values in low-rank MFs
- Interpretation of the factorization in the scope of movie recommendations
- A Netflix prize-winning approach for matrix completion

Part 3: Principal Components Analysis (PCA)
- Finding good low-dimensional representations of the data
- Finding the directions of maximum variance in the data
- Solving the objective of PCA by means of the truncated SVD

Part 4: Notebook
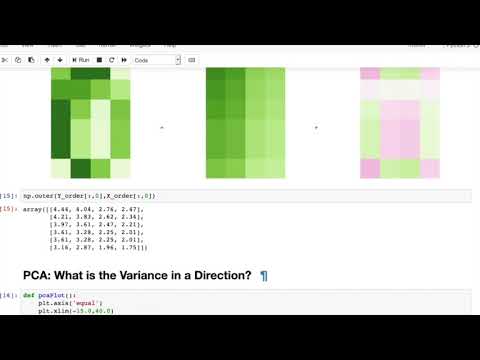
- Visualization of SVD
- Computing the variance of the data in a direction
- Visualization of PCA projections
slides PELi PELi Solutions Notebook
k-means Clustering
within-cluster-scatter - k-means as matrix factorization - alternating minimization
Part 1: The k-means Objective
- The cluster model of k-means
- The k-means objective to minimize the within-cluster-scatter
- The k-means objective is equivalent to minimizing the distance of points to their closest centroid
- Lloyds' algorithm for the optimization of k-means

Part 2: k-means as a Matrix Factorization
- Indicating clusters by a binary matrix
- Computing the centroids in matrix notation
- The k-means objective as a constrained matrix factorization problem

Part 3: k-means Optimization via Block-Coordinate Descent
- Centroids are the minimizes of the k-means objective when fixing the cluster assignments
- Assigning points to the clusters with closest centroid minimizes the k-means objective when we fix the centroids
- Lloyds' algorithm as block-coordinate descent

Part 4: Notebook
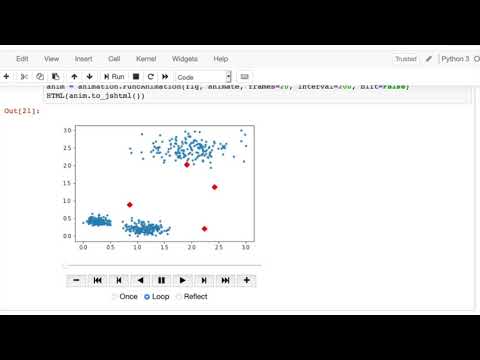
- Visualization of k-means' optimization
- Effect of initialization
- k-means as matrix factorization
slides PELi PELi Solutions Notebook
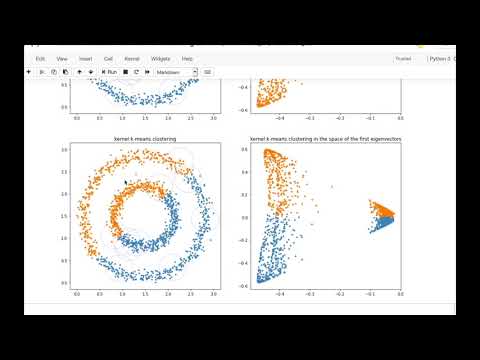
Nonconvex Clustering
kernel k-means - spectral clustering - similarity graph
Part 1: Kernel k-means
- The kernel trick
- RBF kernels
- Optimization challenges
Part 2: Spectral Clustering
- Similarity graph representation of the data
- Minimizing the graph cut
- Graph Laplacians
- Solving spectral clustering via k-means

Part 3: Notebook
- Visualizing the eigendecomposition of the graph Laplacian